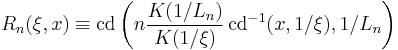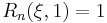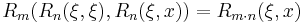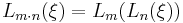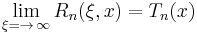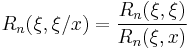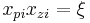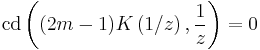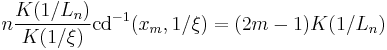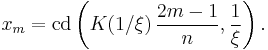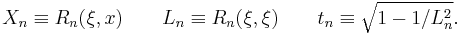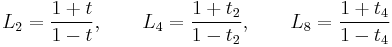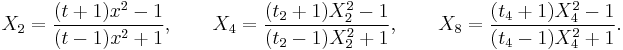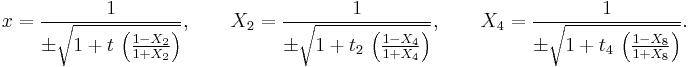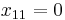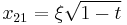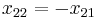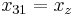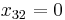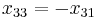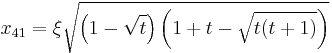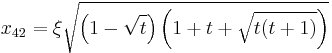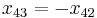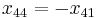Elliptic rational functions
In mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used in the design of elliptic electronic filters. (These functions are sometimes called Chebyshev rational functions, not to be confused with certain other functions of the same name).
Rational elliptic functions are identified by a positive integer order n and include a parameter 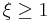 called the selectivity factor. A rational elliptic function of degree n in x with selectivity factor ξ is generally defined as:
called the selectivity factor. A rational elliptic function of degree n in x with selectivity factor ξ is generally defined as:
- cd() is the Jacobi elliptic cosine function.
- K() is a complete elliptic integral of the first kind.
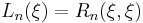 is the discrimination factor, equal to the minimum value of the magnitude of
is the discrimination factor, equal to the minimum value of the magnitude of 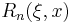 for
for 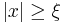 .
.
For many cases, in particular for orders of the form 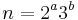 where a and b are integers, the elliptic rational functions can be expressed using algebraic functions alone. Elliptic rational functions are closely related to the Chebyshev polynomials: Just as the circular trigonometric functions are special cases of the Jacobi elliptic functions, so the Chebyshev polynomials are special cases of the elliptic rational functions.
where a and b are integers, the elliptic rational functions can be expressed using algebraic functions alone. Elliptic rational functions are closely related to the Chebyshev polynomials: Just as the circular trigonometric functions are special cases of the Jacobi elliptic functions, so the Chebyshev polynomials are special cases of the elliptic rational functions.
Contents |
Expression as a ratio of polynomials
For even orders, the elliptic rational functions may be expressed as a ratio of two polynomials, both of order n.
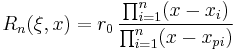 (for n even)
(for n even)
where  are the zeroes and
are the zeroes and 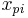 are the poles, and
are the poles, and 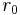 is a normalizing constant chosen such that
is a normalizing constant chosen such that  . The above form would be true for odd orders as well except that for odd orders, there will be a pole at x=∞ and a zero at x=0 so that the above form must be modified to read:
. The above form would be true for odd orders as well except that for odd orders, there will be a pole at x=∞ and a zero at x=0 so that the above form must be modified to read:
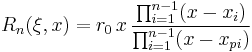 (for n odd)
(for n odd)
Properties
The canonical properties
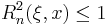 for
for 
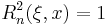 at
at 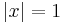
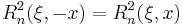
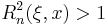 for
for 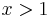
- The slope at x=1 is as large as possible
- The slope at x=1 is larger than the corresponding slope of the Chebyshev polynomial of the same order.
The only rational function satisfying the above properties is the elliptic rational function (Lutovac 2001, § 13.2). The following properties are derived:
Normalization
The elliptic rational function is normalized to unity at x=1:
Nesting property
The nesting property is written:
This is a very important property:
- If
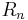 is known for all prime n, then nesting property gives
is known for all prime n, then nesting property gives 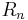 for all n. In particular, since
for all n. In particular, since 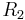 and
and 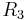 can be expressed in closed form without explicit use of the Jacobi elliptic functions, then all
can be expressed in closed form without explicit use of the Jacobi elliptic functions, then all 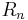 for n of the form
for n of the form 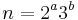 can be so expressed.
can be so expressed. - It follows that if the zeroes of
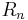 for prime n are known, the zeros of all
for prime n are known, the zeros of all 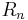 can be found. Using the inversion relationship (see below), the poles can also be found.
can be found. Using the inversion relationship (see below), the poles can also be found. - The nesting property implies the nesting property of the discrimination factor:
Limiting values
The elliptic rational functions are related to the Chebyshev polynomials of the first kind 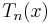 by:
by:
Symmetry
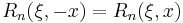 for n even
for n even for n odd
for n odd
Equiripple
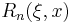 has equal ripple of
has equal ripple of 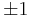 in the interval
in the interval 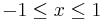 . By the inversion relationship (see below), it follows that
. By the inversion relationship (see below), it follows that 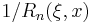 has equiripple in
has equiripple in 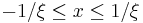 of
of 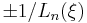 .
.
Inversion relationship
The following inversion relationship holds:
This implies that poles and zeroes come in pairs such that
Odd order functions will have a zero at x=0 and a corresponding pole at infinity.
Poles and Zeroes
The zeroes of the elliptic rational function of order n will be written 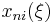 or
or 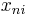 when
when 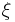 is implicitly known. The zeroes of the elliptic rational function will be the zeroes of the polynomial in the numerator of the function.
is implicitly known. The zeroes of the elliptic rational function will be the zeroes of the polynomial in the numerator of the function.
The following derivation of the zeroes of the elliptic rational function is analogous to that of determining the zeroes of the Chebyshev polynomials (Lutovac 2001, § 12.6). Using the fact that for any z
the defining equation for the elliptic rational functions implies that
so that the zeroes are given by
Using the inversion relationship, the poles may then be calculated.
From the nesting property, if the zeroes of 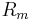 and
and 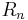 can be algebraically expressed (i.e. without the need for calculating the Jacobi ellipse functions) then the zeroes of
can be algebraically expressed (i.e. without the need for calculating the Jacobi ellipse functions) then the zeroes of 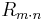 can be algebraically expressed. In particular, the zeroes of elliptic rational functions of order
can be algebraically expressed. In particular, the zeroes of elliptic rational functions of order 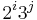 may be algebraically expressed (Lutovac 2001, § 12.9, 13.9). For example, we can find the zeroes of
may be algebraically expressed (Lutovac 2001, § 12.9, 13.9). For example, we can find the zeroes of 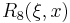 as follows: Define
as follows: Define
Then, from the nesting property and knowing that
where 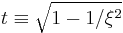 we have:
we have:
These last three equations may be inverted:
To calculate the zeroes of 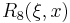 we set
we set 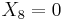 in the third equation, calculate the two values of
in the third equation, calculate the two values of 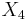 , then use these values of
, then use these values of 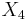 in the second equation to calculate four values of
in the second equation to calculate four values of 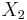 and finally, use these values in the first equation to calculate the eight zeroes of
and finally, use these values in the first equation to calculate the eight zeroes of 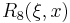 . (The
. (The 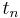 are calculated by a similar recursion.) Again, using the inversion relationship, these zeroes can be used to calculate the poles.
are calculated by a similar recursion.) Again, using the inversion relationship, these zeroes can be used to calculate the poles.
Particular values
We may write the first few elliptic rational functions as:
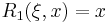
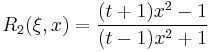
-
- where
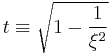
-
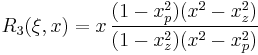
-
- where
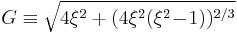
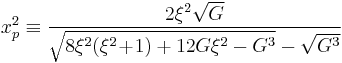
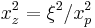
-
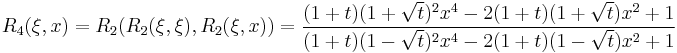
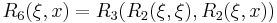 etc.
etc.
See Lutovac (2001, § 13) for further explicit expressions of order n=5 and 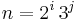 .
.
The corresponding discrimination factors are:
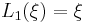
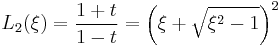
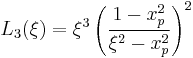
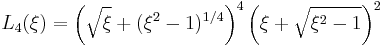
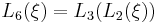 etc.
etc.
The corresponding zeroes are 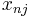 where n is the order and j is the number of the zero. There will be a total of n zeroes for each order.
where n is the order and j is the number of the zero. There will be a total of n zeroes for each order.
From the inversion relationship, the corresponding poles 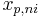 may be found by
may be found by 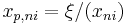
References
- Daniels, Richard W. (1974). Approximation Methods for Electronic Filter Design. New York: McGraw-Hill. ISBN 0-07-015308-6.
- Lutovac, Miroslav D.; Tosic, Dejan V., Evans, Brian L. (2001). Filter Design for Signal Processing using MATLAB© and Mathematica©. New Jersey, USA: Prentice Hall. ISBN 0-201-36130-2.